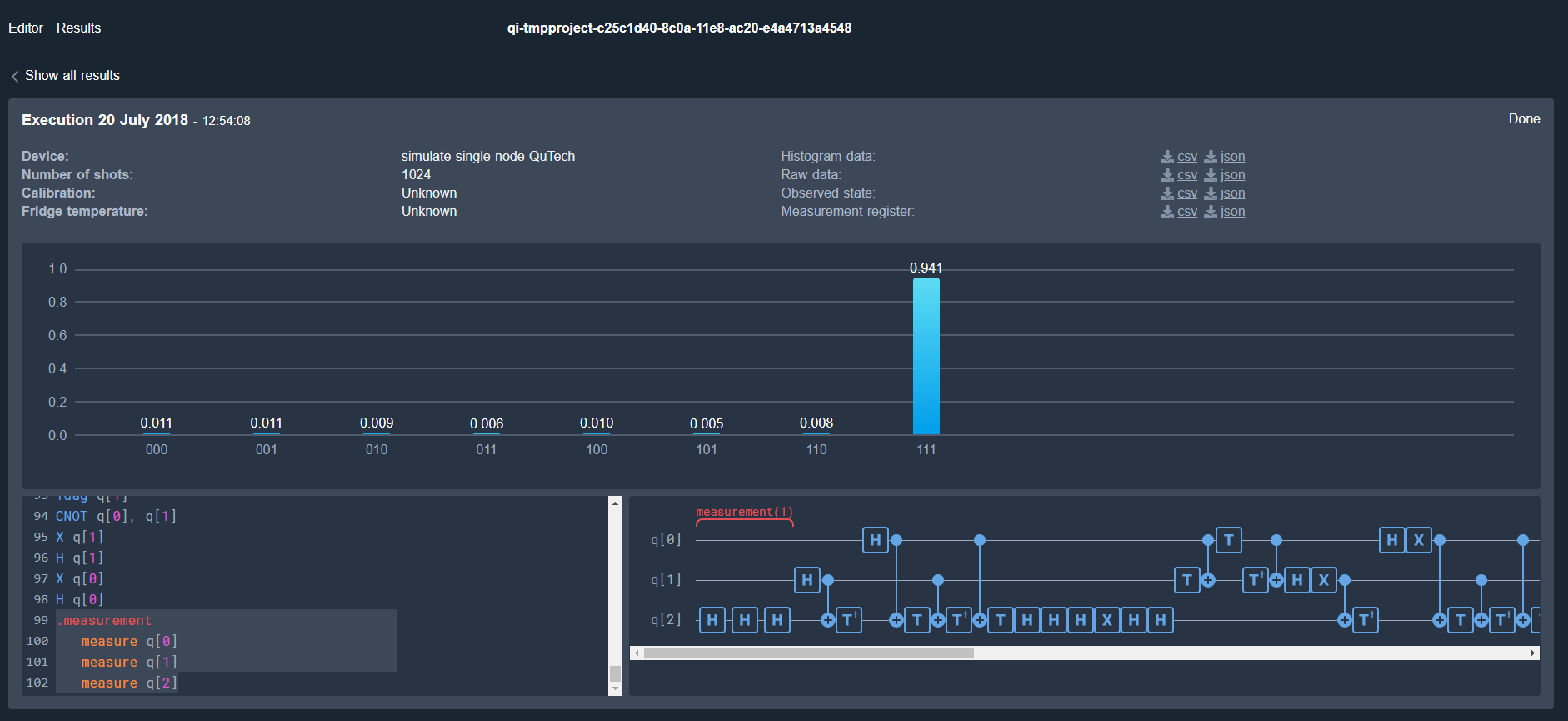
n=3
N=2**n
q = QuantumRegister(n)
qc = QuantumCircuit(q)
if n==1:
def black_box(qc, q):
qc.z(q)
elif n==2:
def black_box(qc, q):
for i in range(n):
qc.s(q[i])
qc.h(q[1])
qc.cx(q[0], q[1])
qc.h(q[1])
for i in range(n):
qc.s(q[i])
else:
def black_box(qc, q):
qc.h(q[2])
qc.ccx(q[0], q[1], q[2])
qc.h(q[2])
black_box(qc,q)
cplot=qc.draw(output='mpl')
display(cplot)
print('black box circuit:')
run_circuit(qc, q)
black box circuit: